Немного про ГРИП

Формулы расчёта в данном калькуляторе неизвестны(

--

оказывается, грипы разные бывают :D

http://www.zenitcamera.com/qa/qa-dof.html

Цитата:

от: uopp
Формулы расчёта в данном калькуляторе неизвестны(

--

оказывается, грипы разные бывают :D

http://www.zenitcamera.com/qa/qa-dof.html

М-да... Поговорили немного, полтора десятка страниц, о проблеме, которая выеденного яйца не стоит...
Поймите наконец, границ резкости не существует, их каждый рисует в меру своего понимания и они, по большому счёту, на самом деле никому не нужны в фотографии. А вот какого размера детали будут различимы, а какого нет - нужно знать любому фотографу, который вырос из простого кнопконажимателя.

ненене! они есть, но кмк используемые в т.ч. в этом топике формулы используют коэффициенты плёночной эпохи. "допустимый размер пятна вместо точки" вот какой должен быть насейчас, например, у матрицы пядвака али olympus e-520?
а сие один из коэфф. формул.

Цитата:

от:uopp
ненене! они есть, но кмк используемые в т.ч. в этом топике формулы используют коэффициенты плёночной эпохи. "допустимый размер пятна вместо точки" вот какой должен быть насейчас, например, у матрицы пядвака али olympus e-520?
а сие один из коэфф. формул.

Подробнее

Так это границы применимости, какое разрешение предельно и больше не будет, что определяется свойствами системы в целом, а что точно не будет различимо на сцене независимо от свойств оптики-матрицы и что можно будет увидеть на снимке - вот что интересно.
Впрочем, если кто молится на границы - ради бога, "у каждного свой вукус". Просто это крайне неудобно и невероятно сложно посчитать, о расчётах в уме не может быть и речи. Ну, получили границы... И что, много пользы от этого? А насколько будут размыты детали (структура) вне зоны ГРИП? А какие детали будут ещё различимы на этой самой границе? А на половине расстояния до границы? Нет ответа...

Цитата:

от:alexandrd
Просто это крайне неудобно и невероятно сложно посчитать, о расчётах в уме не может быть и речи. Ну, получили границы... И что, много пользы от этого? А насколько будут размыты детали (структура) вне зоны ГРИП? А какие детали будут ещё различимы на этой самой границе? А на половине расстояния до границы? Нет ответа...

Подробнее

ответ есть. просто надо внимательнее читать топик. я приводил ссылку несколько страниц назад. могу ее повторить

Цитата:

от:Relayer
ответ есть. просто надо внимательнее читать топик. я приводил ссылку несколько страниц назад. могу ее повторить

Подробнее

А зачем ту ссылку читать, если там чепуха в выкладках?

Написано:

c' - диаметр пятна, в которое размывается бесконечно удаленная точка
c' = f 2/(dN)


Т.е. это вроде бы допустимый кружок рассеяния на гиперфокальном. Ну пусть. Дальше чепуха:

c' = f 2/(dN) = (Mf)/N;

Потому что:
M - масштаб съемки (M = f / d).

А мы же знаем, что при d=2f M=1, что ну никак не получается по формуле. К тому же, при d=бесконечности М=0 и c' тоже.

Менее заметная, но значительно более существенная чепуха вот тут:

c = c' * | 1 - d / d0 |,
Две вертикальные черты |…| обозначают операцию вычисления абсолютной величины числа.

Таким образом, при d < d0 c < = c', а при d=d0 с=0, т.е. в любом таком случае меньше диаметра пятна, в которое размывается бесконечно удаленная точка, согласно определению автора. При некотором d > 2d0 c > c' и с увеличением d растет. При фокусировке d в бесконечность d0 (текущая дистанция) все равно какая, но с= бесконечности. Ну никак на картинку не похоже. Если же считать, что в бесконечности c'=0, чтобы получилась неопределенность, то не ясно, с какого боку тут приплести резкость. По источнику http://hobbymaker.narod.ru/Articles/sharpness_rus.htm резкость выбирается по вкусу, что никак не лучше классической оценки, хотя источник новые подходы усиленно рекламирует. Поэтому и возникают вот такие откровения:

3. Вопреки классической теории, Мерклингер утверждает, что область резкости всегда расположена симметрично относительно объекта съемки.

Ну и пусть утверждает. Кроме него, все остальные знают, что область резкости всегда расположена НЕсимметрично относительно объекта съемки. Зачем продвигать теорию, не соответствующую опыту и более того, собственным же исходным положениям?

Цитата:

от:zzy
По источнику http://hobbymaker.narod.ru/Articles/sharpness_rus.htm резкость выбирается по вкусу, что никак не лучше классической оценки, хотя источник новые подходы усиленно рекламирует. Поэтому и возникают вот такие откровения:

3. Вопреки классической теории, Мерклингер утверждает, что область резкости всегда расположена симметрично относительно объекта съемки.

Подробнее

Что, мягко выражаясь, не совсем так, Мерклингер учитывает дифракцию, что сразу приводит к несиммеричности области резкости.
Цитата:

от: zzy

Ну и пусть утверждает. Кроме него, все остальные знают, что область резкости всегда расположена НЕсимметрично относительно объекта съемки.

Естественно. А насколько несиммерична?
Дело в том, что метод Мерклингера аппроксимационный, дающий достаточную для практики точность. И такой вопрос: Вам действительно важно знать, что на расстоянии, к примеру, 10 метров одинаковое размытие (резкость) будет не на +-1м, а на +1 и -0,979м?
Кстати, в ближней от фокусировки зоне в обе стороны метод имеет некоторый запас по дифракционному разрешению из-за линеаризации кривой.
Можно возразить, что есть случай фокусировки на гиперфокал, где асимметрия чудовищно не совпадает с Мерклингеровской линеаризацией. А велика ли эта "чудовищность"? Если перевести рассмотрение в пространство предметов - то, чем дальше - тем метод точнее.
Итого: метод достаточно точен в ближней от фокусировки зоне (расстояние рассмотрения, от точки фокусировки, << расстояния фокусировки) и в дальней зоне (расстояние рассмотрения >> расстояния фокусировки) и имеет допусимую погрешность в средней зоне.
Что и требуется на практике.

Цитата:

от:zzy
По источнику http://hobbymaker.narod.ru/Articles/sharpness_rus.htm резкость выбирается по вкусу, что никак не лучше классической оценки, хотя источник новые подходы усиленно рекламирует. Поэтому и возникают вот такие откровения:

3. Вопреки классической теории, Мерклингер утверждает, что область резкости всегда расположена симметрично относительно объекта съемки.

Подробнее

Что, мягко выражаясь, не совсем так, Мерклингер учитывает дифракцию, что сразу приводит к несиммеричности области резкости.
Цитата:

от: zzy

Ну и пусть утверждает. Кроме него, все остальные знают, что область резкости всегда расположена НЕсимметрично относительно объекта съемки.

Естественно. А насколько несиммерична?
Дело в том, что метод Мерклингера аппроксимационный, дающий достаточную для практики точность. И такой вопрос: Вам действительно важно знать, что на расстоянии, к примеру, 10 метров одинаковое размытие (резкость) будет не на +-1м, а на +1 и -0,979м?
Кстати, в ближней от фокусировки зоне в обе стороны метод имеет некоторый запас по дифракционному разрешению из-за линеаризации кривой.
Можно возразить, что есть случай фокусировки на гиперфокал, где асимметрия чудовищно не совпадает с Мерклингеровской линеаризацией. А велика ли эта &quot;чудовищность&quot;? Если перевести рассмотрение в пространство предметов - то, чем дальше - тем метод точнее.
Итого: метод достаточно точен в ближней от фокусировки зоне (расстояние рассмотрения, от точки фокусировки, гораздо меньше расстояния фокусировки) и в дальней зоне (расстояние рассмотрения гораздо больше расстояния фокусировки) и имеет допусимую погрешность в средней зоне.
Что и требуется на практике.

Цитата:

от:zzy
Дальше чепуха:
c' = f 2/(dN) = (Mf)/N;
Потому что:
M - масштаб съемки (M = f / d).
А мы же знаем, что при d=2f M=1, что ну никак не получается по формуле. К тому же, при d=бесконечности М=0 и c' тоже.

Подробнее

Если расстояние фокусировки существенно превышает фокусное расстояние объектива (что чаще всего справедливо), то масштаб M определяется следующей приближенной формулой:
M = f / d.
это общеизвестный факт и странно что вы его не знаете. в данном случае такая формулировка нас устраивает и погрешность крайне незначительна

Цитата:

от:zzy
Менее заметная, но значительно более существенная чепуха вот тут:
c = c' * | 1 - d / d0 |,
Две вертикальные черты |…| обозначают операцию вычисления абсолютной величины числа.
Таким образом, при d < d0 c < = c', а при d=d0 с=0, т.е. в любом таком случае меньше диаметра пятна, в которое размывается бесконечно удаленная точка, согласно определению автора. При некотором d > 2d0 c > c' и с увеличением d растет. При фокусировке d в бесконечность d0 (текущая дистанция) все равно какая, но с= бесконечности. Ну никак на картинку не похоже. Если же считать, что в бесконечности c'=0, чтобы получилась неопределенность, то не ясно, с какого боку тут приплести резкость

Подробнее

c' = f^2/(d*N)
c = c' * |1 - d/d0|

c = f^2 * |1 - d/d0| / (d*N)

возьмем предел при d стремящемся к бесконечности и раскроем неопределенность

lim c = lim f^2 * |1 - d/d0| / (d*N) = lim f^2 * | 1/d - d/(d*d0) | / N =
= f^2 * | - 1/d0 | / N = f^2 / (N*d0)

т.е. при фокусировке в бесконечность размытие c будет обратно пропорционально d0. что и нарисовано на следующем графике

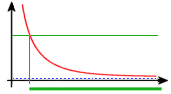
Объектив сфокусирован на бесконечность. Чем ближе объект расположен к камере, тем сильнее он размыт. Ближняя граница зоны резкости совпадает с гиперфокальным расстоянием.
http://hobbymaker.narod.ru/Articles/sharpness_rus.htm

математику, хотя бы в объеме начал анализа, необходимо знать. особенно если вы решили оперировать бесконечностями.

Цитата:

от: zzy
А зачем ту ссылку читать, если там чепуха в выкладках?

там все правильно и соответствует практически-наблюдаемым вещам. просто надо включать моск при прочтении.

о чом вобще базар - размытие в пространтсве предметов ЛИНЕЙНО!!

т.е. метод позволяет задать 2 точки с заданым размытием ПРЕДМЕТОВ и оттуда получить ТОЧНУЮ наводку и диафрагму. фсё.

зачем требовать одинаковое размытие предметов на ближней и дальней плане этодругой вопоср!!11 но сколько затребовать столько и получиться это факт!!

что б получить размытие на плёнке надо фсё тупо поделить на расстояние и фсё.
вместо расстояния будет открутка по шкале на объективе и фсё.

Прочитал это все и понял.

Школьное образование в РОссии - ничто по сравнению с СССР!
мало того
ДВоешников в фотографии столько, что мама не горюй.
И это удивительно, ибо именно фотография требует определенного багажа знаний. Впрочем, цифровая - нет. Жми кнобку да и все...

Господи! Родные мои! Вы многословно и многоумственно путаете 2 величины, которые между собой НИКАК не совместимы.
Вы сравниваете линейную характеристику оптики и угловую.
Т.е. - для простоты - метры и градусы.
А для тех, кто в бронепоезде - длинну и температуру кипения.

Блин... Министру образования надо клистер поставить. Из скипедара с патефонными иголками. Надо же!
Хоть бы по размерности бы посчитали - как это мм = град?!!!

Видел даже чертеж-схему с умным объяснением. Ну почему бы не продолжить эту схему - и не нарисовать приемник? А? А потом - нарисовать МЕНЬШИЙ приемник в той же фокальной плоскости? и не увидеть (глазками! А кто не верит - пощупать ручками), что линейный параметр ГРИП, завязанный на оптическую систему, никак не связан с угловым параметром, отличающий КРОП от ФФ...

И как вы все аттестат получили?! За бабки небось.. А тут, наверное, и ВО есть люди? Тоже - куплены, наверное, дипломы...

да йа хренею уже лимиты лимитить начали... да весь этот гриб выеденого ейца нестоит..
щкала предметов размытие = диаметр * расстояние [*масштаб с\ёмки] фсё
угловая щкала размытие = диаметр * дефокус [*зум]
фсё

Цитата:

от:arristo
Школьное образование в РОссии - ничто по сравнению с СССР!
мало того
ДВоешников в фотографии столько, что мама не горюй.
И это удивительно, ибо именно фотография требует определенного багажа знаний. Впрочем, цифровая - нет. Жми кнобку да и все...

Блин... Министру образования надо клистер поставить. Из скипедара с патефонными иголками. Надо же!
Хоть бы по размерности бы посчитали - как это мм = град?!!!

Подробнее

В 1949 г. на юбилейной сессии Академии наук в Ленинграде, посвященной 225-летию ее основания, была продемонстрирована исключительная роль русской науки в истории человечества. Опора на собственные силы и попытка находить оригинальные решения, идти собственным путем дала выдающийся результат в резком научном и технологическом рывке, совершенном СССР в 50-60-е годы.

А вспомните, что стало ныне, после победы демократии? Окончательно скисли и практически исчезли замечательные научно-популярные журналы, которыми духовно питались поколения 50-60-х, народ повернулся слушать Чумака и Кашпировского, а потом и вовсе ударился в ворожбу и волхвование

С.Миронин, "Сталинский порядок".

Цитата:

от:Relayer
математику, хотя бы в объеме начал анализа, необходимо знать. особенно если вы решили оперировать бесконечностями.

там все правильно и соответствует практически-наблюдаемым вещам. просто надо включать моск при прочтении.

Подробнее

Понятно и так, что там оба с в бесконечности на асимптоту выйдут. В нуль. Асимптотой для с будет с', а оно в свою очередь ->0 при d -> к бесконечности. Ну, и хорошо. Вопрос же не в этом, а в том, где же тут резкость? Отсутствует критерий, по которому резкое изображение отличается от нерезкого.

Что сразу приводит к шаманизму. Т.е. критерий-то надо вводить, но лучше кружка рассеяния придумать не удается. С какого-то боку начинают приплетать дифракцию, когда-нибудь доберутся и до черных дыр. :( А при чем тут та дифракция, если у цифроматричной техники хроматизм и астигматизм немерянные? Вот такого рода выкладки, которые энергично обсуждаются, отлично маскируют принципиальные недостатки цифротехники. Типа, ребята, да оно забугорное - значит, отличное, покупайте. А что не получается - так это классические формулы кривые. :(

Цитата:

от:arristo
Прочитал это все и понял.

Школьное образование в РОссии - ничто по сравнению с СССР!
мало того
ДВоешников в фотографии столько, что мама не горюй.
И это удивительно, ибо именно фотография требует определенного багажа знаний. Впрочем, цифровая - нет. Жми кнобку да и все...

Подробнее

Немного не так. Цифровая фотография как раз и показала уровень фотографического образования, который и во времена СССР был далеко не так высок, как предполагало получение среднего образования. Байты и пиксели. Биты и ДД. И многое другое, в чём откровенно плавают даже те, кто считает себя профи...
Неумение встать по другую сторону объектива, в пространство предметов и оценить всю сцену на предмет размытия и разрешения - чёткий диагноз всей нашей фотографической камарильи... :cannabis:
Цитата:

от:arristo

Господи! Родные мои! Вы многословно и многоумственно путаете 2 величины, которые между собой НИКАК не совместимы.
Вы сравниваете линейную характеристику оптики и угловую.
Т.е. - для простоты - метры и градусы.
А для тех, кто в бронепоезде - длинну и температуру кипения.

Блин... Министру образования надо клистер поставить. Из скипедара с патефонными иголками. Надо же!
Хоть бы по размерности бы посчитали - как это мм = град?!!!

Подробнее

Не, здесь всё сложнее, спирт 96 градусов, вода кипит при 100 градусах, а прямой угол - 90 градусов...

Как тут не запутаться...

Цитата:

от: zzy
Вопрос же не в этом, а в том, где же тут резкость? Отсутствует критерий, по которому резкое изображение отличается от нерезкого.

читайте внимательно: резкость - на отпечатке.
если не понятно, то берем среднестатистически-слепого зрителя, усаживаем его на расстоянии оптимального рассматривания от отпечатка и внимательно его слушаем. делим на увеличение отпечатка - получаем тот самый предельный кружок за которым уже не особо резко.

основная проблема 99% фотографов, рассуждающих о ГРИП (или упаси господи ваяющих ГРИП-кулькуляторы) заключается в том что они не понимают то как ведет себя кружок рассеяния в зависимости от положения точки относительно фокуса. распространенное заблуждение - в ГРИП все резко, а чуть влево-вправо - усе, ниреско. ага. щаз.

вот поэтому и нужны графики. поэтому и нужны формулы которые дают не границу ГРИП, а диаметр кружка рассеяния для произвольной точки. и это позволяет ответить например на такой вопрос - если фокус на глазах , то насколько ниреско будут выглядеть ухи расположенные на среднестатистической голове. или насколько вхлам размоется подружка которая стот позади в метре? в двух? за амбаром?

Цитата:

от:Relayer
читайте внимательно: резкость - на отпечатке.
если не понятно, то берем среднестатистически-слепого зрителя, усаживаем его на расстоянии оптимального рассматривания от отпечатка и внимательно его слушаем. делим на увеличение отпечатка - получаем тот самый предельный кружок за которым уже не особо резко.

Подробнее

Если бы было так просто...
А я, например, хочу, чтобы номер машины на заднем плане был наоборот, не читаем, вхлам... А ближе в три раза - наоборот, читаем без проблем, но всё равно за пределами ГРИП... И чем мне помогут слепые ГРИПоуловители?
Любит народ у нас всё делать задом наперёд, сначала получает изображение, а потом рассуждает о том, что же там получилось, где там знаменитый среди фотографов кружок, о котором все судачат на форумах??
А слабо сразу предсказать, что должно получиться, ещё даже без камеры и заглядывания в видоискатель?
Цитата:

от:Relayer


основная проблема 99% фотографов, рассуждающих о ГРИП (или упаси господи ваяющих ГРИП-кулькуляторы) заключается в том что они не понимают то как ведет себя кружок рассеяния в зависимости от положения точки относительно фокуса. распространенное заблуждение - в ГРИП все резко, а чуть влево-вправо - усе, ниреско. ага. щаз.

вот поэтому и нужны графики. поэтому и нужны формулы которые дают не границу ГРИП, а диаметр кружка рассеяния для произвольной точки. и это позволяет ответить например на такой вопрос - если фокус на глазах , то насколько ниреско будут выглядеть ухи расположенные на среднестатистической голове. или насколько вхлам размоется подружка которая стот позади в метре? в двух? за амбаром?

Подробнее

Так метод Мерклингера и даёт ответы на эти вопросы... И никаких графиков...
Правда, есть тонкости. Например, пятно от точки в одном объективе имеет вид Гауссова распределения, в другом - похоже на меандр, в третьем - вообще на бублик и т.д. А в цифре все точки похожи на кирпичи. Видимо, не даром так популярны снимки кирпичных стен...

Господи! Ну сколько можно уже об одном и том же баянить!
Метод Меркглингера хорош для судмедэкспертизы! Для фотографии, которая хоть как-то претендует на долю художественности, достаточно заглянуть в видоискатель и прикрыть диафрагму!

это работает токо на цыфромыле формата дваждыкроп и мельче хДДДДДДДДДДД

Цитата:

от:Nanto
Господи! Ну сколько можно уже об одном и том же баянить!
Метод Меркглингера хорош для судмедэкспертизы! Для фотографии, которая хоть как-то претендует на долю художественности, достаточно заглянуть в видоискатель и прикрыть диафрагму!

Подробнее

Ну-да... Ну-да... Если глаз как у орла...
На практике приличный по разрешению электронный видоискатель с увеличением при фокусировке ещё позволяет что-то рассмотреть, а про зеркалки можете песни не петь... Закрыть диафрагму, ага... до 11-ти... И потом утверждать, что там Граница РИП прям чуть ли не красной линией нарисована... :cannabis: